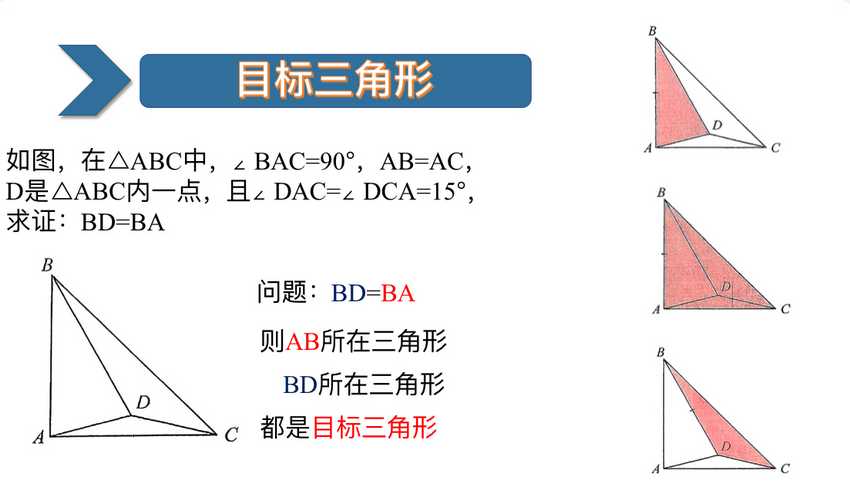
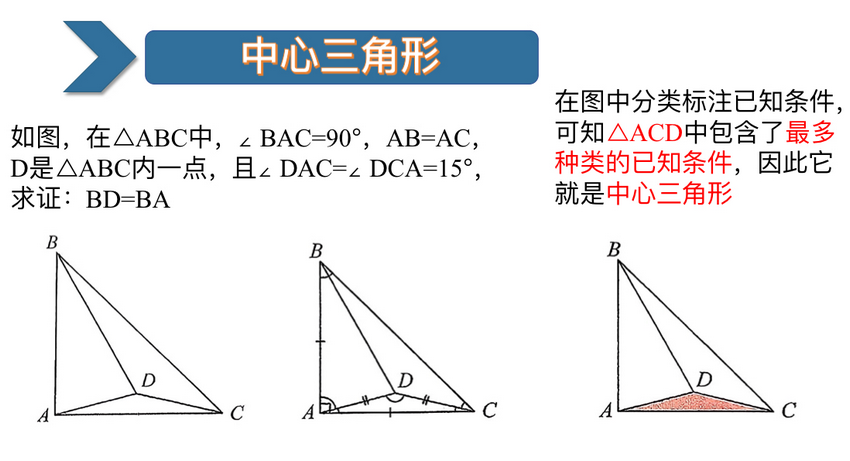
分享中，白兆敏老师以几何难题“已知条件与解题目标关联隐蔽”的痛点为切入点，首次明确“关键三角形”的双重定义：既包含与解题目标直接相关边或角的“目标三角形”，也涵盖拥有最多已知条件的“中心三角形”。通过两道经典例题——“等腰直角三角形内证BD=BA”与“锐角三角形内证ED平分∠FEC”，主讲人现场演示如何通过分类标注已知条件，快速锁定关键三角形，让复杂图形的核心关联一目了然。

　　针对三角形构造这一核心环节，分享活动创新性地提出“全等贴靠、相似贴靠、内切、外补”四大构造方法，并结合全国“祖冲之”杯邀请赛真题、几何综合题等典型案例，直观呈现构造逻辑。以“∠A=20°、∠B=80°且AD=BC，求∠BDC”为例，主讲人通过“构造等边△ACE”“等腰△ABE”的全等贴靠操作，清晰推导解题路径；在“证DC=BC”的综合题中，更是展示了“对折贴靠构造等边△AFC”“内切构造等边△OBC”“外补构造等腰△CAM”等四种差异化解法，生动诠释了“构造之趣源于思考”的理念。

　　活动特别强调“中心三角形的阶段性”这一关键认知，提醒学习者需随已知条件推导动态更新关键三角形，避免陷入固定思维。现场演示的“无效构造排除法”，更让参与者掌握了“以增加关联为核心”的构造判断标准，有效提升了解题效率。

　　此次分享打破了传统几何解题的“题海战术”模式，以“关联分析+精准构造”为核心，为初中几何学习提供了可复制、可迁移的思维工具。不少参与者表示，这种“从关键图形切入、以构造方法破题”的思路，让原本复杂的几何题变得有章可循，为后续学习打开了新视野。